#factoftheweek
How to explain what a quant does!
Week #22: Have you ever tried explaining to your friends or family what a quant is and does? This week we advice you to take a look at Investopedia, since they have a great and brief explanation in this article, written by Tristan Yates. "As financial securities become increasingly complex, demand has grown steadily for …
Choosing method!
Week #21: It is all about finding the right method, and as a quant you will be able to choose the right one. This week is the initial #factoftheweek. For future posts, stay put!
The relevant subjects are continuously covered in the above menu "Topics". If you think something is missing, feel free to stop by later.
Probability Theory
The basics of Probability Theory
(Updated May 27, 2017)
When looking at certain models, we often want to know the probability that a certain event will occur. In these models we may look at different subjects which have different variability, i.e. different characteristics. Each model is approximative and only describes the most relevant characteristics. In finance we talk about abstract models, either deterministic or stochastic. Probability theory in financial mathematics is the basic building block of algorithms, risk calculations etc.
#1 Events
The amount of possible outcomes is called the sample space: 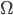 .
.
The possible outcomes 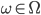 .
.
Events are subsets  of the sample space.
of the sample space.
Portfolio Theory
Choosing the right portfolio
(Updated May 22, 2017)
Useful methods when deciding on investments and risk can be set up by simple mathematics with support of linear algebra and probability. It is however difficult to choose which historical data to model the future on, since that data is the result of individual actions and random events. The portfolio is in the end chosen with the outset of individual subjective probability and opinion on risk. With the help of probability distributions, we can push these individual actions in the right direction.
#1 Compounding
The principal is the original amount of capital invested or borrowed. The principal plus gained interest rate, together gives an exponential interest rate called "interest on interest".
Yearly compounding: 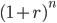
Monthly compounding: 
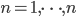
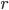 is the interest rate.
is the interest rate.
Continuous compounding means letting equally long time periods 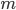 tend to infinity.
tend to infinity.
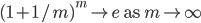
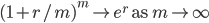
Continuous compounding does not give out much higher total interest than traditional compounding. However since continuous compounding is widely important in finance, we will refer interest rates on this blog to continuous compounding unless stated otherwise.
#2 Deterministic Cash Flows
A deterministic cash flow is a set 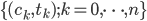 of pairs
of pairs 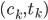 , where
, where 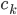 represents the cash received at time
represents the cash received at time 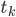
Remember:
Positive cashflow = inflow of money
Negative cash-flow = outflow of money
The present value of a stream of cash flows 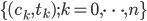 is:
is:
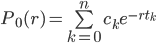
…and the future value is:
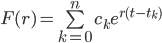
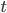 is the time.
is the time.
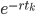 is the discount factor.
is the discount factor.
Note that 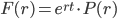 .
.
If there exists an interest rate  such that
such that 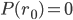 , then we call
, then we call  the internal rate of return (IRR) of the stream of cash flows.
the internal rate of return (IRR) of the stream of cash flows.
A bond (with and without coupons) usually has a unique and positive IRR, and it is called the yield-to-maturity (YTM) of the bond.
When the bond is a zero-coupon bond with maturity time 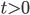 and with face value
and with face value 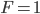 , we can easily solve for its YTM which we call
, we can easily solve for its YTM which we call 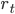 .
.
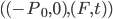 cashflows for this bond.
cashflows for this bond.
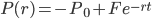
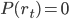
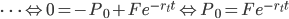
 is the YTM for the zero coupon bond. The interest rate
is the YTM for the zero coupon bond. The interest rate 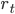 is called the t-year zero rate or spot rate.
is called the t-year zero rate or spot rate.
Arbitrage opportunity: Streams of cash flows that are better than others, e.g.
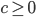 and
and 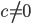 .
.
#3 Arbitrage-Free Cash Flows
An arbitrage-free price of an instrument paying 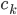 at time
at time 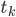 for
for 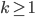 is
is
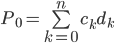
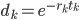 is the discount factor, where
is the discount factor, where 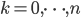 .
.
#4 The lognormal model
A popular model where the price of the asset at time 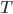 is given by:
is given by:
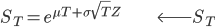 is lognormally distributed here.
is lognormally distributed here.
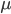 is the mean.
is the mean.
 is the standard deviation.
is the standard deviation.
 .
.
Hence: 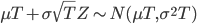
#5 M.V.P. (minimum variance portfolio)
Portfolio with smallest variance.
We want to solve:

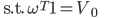 (units of currency/initial wealth)
(units of currency/initial wealth)
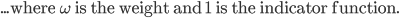
The Lagrangian in this case: 
#6 E.S. (expected shortfall)
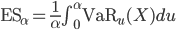
#7 Betting
Arrow-Pratt's absolute risk aversion coefficient:
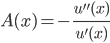
#8 Quadratic hedging
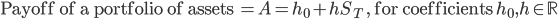

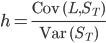
Solve problems of the type 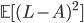
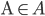 , where
, where  is a set of available asset payoffs.
is a set of available asset payoffs.
Risk Management
Risk based on historical data
(Updated May 22, 2017)
When modeling risk we look at a set of historical data to model the value at a future time T > 0. E.g. bond prices, share prices, claim sizes or exchange rates.
Historical share prices may not be good representatives of possible future share prices. Instead we will look at samples of historical returns, which may be good representatives of possible future returns over the next time period. Historical zero rates will also be interesting to analyze in this case.
The subjective approach to modeling the future will be investigated in this post and we will start with sample preparation.
Let us jump to it!
The share price may be strongly dependent on the previous day's price. The sample of historical asset prices may be transformed into a sample of vectors of returns. However, it is not essential for sample preparation to work. We could replace the returns with price differences instead, if we wanted to.
The essential point is just to:
- Take the original sample.
- Transform the original sample to another sample.
- Transform that other sample to a sample whose points may be viewed as independent copies of the future portfolio value.
And now on to the word empirical (greek word).
#1 Empirical Distributions
The distribution function of observations x1,…,x2.
#2 Empirical Qunatiles
#3 Empirical VaR and ES
#4 Selecting a Parametric Model
Mathematical Statistics
Simulating statistical data using the methods Monte Carlo, Markov Chain Monte Carlo and Bayesian Interference
(Updated May 26, 2017)
We often want to compute some kind of expectation:
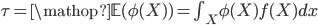
Program Construction in C++
Build a program with algorithms
(Updated May 22, 2017)
Scientific computing is widely applied in finance and program construction is the essential ingredient to make this job easier. What you want is to create simulations, i.e. recreating real-world systems in a controlled environment. To achieve a computer simulation of a physical process, the five step process is to:
- Identify the physical process.
- Formulate a mathematical model for the process.
- Then select or design an algorithm for the given model.
- The algorithm is then translated into software, in this case C++.
- Voilà, the simulation results can be obtained by running simulations!
The software needs to be correct, efficient, easily maintainable and easy extendible. Efficient code might be even more important in financial systems. If someone needs to dive into the software to either upgrade or maintain it, it should be clear what everything is.
Being a quant or software engineer also pushes you to certain requirements, you need to:
- Understand the mathematical problem.
- Understand numerics.
- Designing algorithms and data structures.
- Selecting and using libraries and programming tools.
- Verify the correctness of the result.
- Quickly learn new programming languages.
What Languages should we speak?
In Scientific Computing, a few programming languages received wider attention, e.g.:
- Fortran (77, 95, 2003, 2008).
- C.
- C++.
- Matlab (Octave).
- Python.
- Maple/Mathematica.
When choosing a programming language, these aspects are taken into consideration:
- Computational efficiency.
- Costs of development cycle, maintainability.
- Built-in high performance utilities.
- Support for user-defined data types.
For different parts of the project, different programming languages may be more suitable. Interoperability.
#1 C++ Class
A C++ class is a programmatic description of a data type, which is an abstract and finite set with including operators.
Either as:
- class, which is public.
- struct, which is private.
A C++ class name usually start with a capital letter.
#2 C++ Data Types
Integer types: int
Float types: double
Pointers
References
Void
#3 The main Function
Every program must have exactly one.
int main()
Instead of using return arguments, it is more safe to use predefined variables at the end of the program: EXIT_SUCCESS, EXIT_FAILURE etc.
#4 Basic Input/Output (I/O)
Organized by using streams.
#5 Grids
Class for handling computational domains approximating PDE's by algebraic equations. You can call it a subdivision of domain into small cells or a finite set of points intended for approximating PDE's. They are either structured or unstructured.
#6 Unstructured Grid
- Handles complex geometries
- "Straightforward" generation and refinement.
However, it is inefficient because of indirect addressing (inefficient cache usage, many dereferences).
#7 Structured Grid
Indexed along coordinate axes.
#8 Namespaces
Every name belong to a namespace, which are used to avoid collisions between identifiers in libraries and our own definitions. E.g., names of the C++ standard libraries, belongs to the namespace std.
#9 Pointers
An object containing an address of main memory. A pointer is allowed to "point" to objects of certain type.
Definition: type *p;
#10 Constructors
Determines what happens if an instance of a class (an object) is created. Built in data-types have default contructors, e.g. a statement int i. The initial value for one instance of a built in data-type is undefined.
Copy Constructor.
int = 0 invokes the copy constructor, it's aim is to initialize an instance of a class by another instance of the same class. The copy constructor is also invoked when:
- objects are defined by =, or class(objects of that class).
- objects are passed as actual parameters for non-reference arguments.
- returning objects from a function that has a non-reference return type.
#11 Destructor
Inverse operation of constructors, destructors do whatever work needed to free the resources used by an object.
#12 Operator Overloading
Means that operators can be redefined for new data types. The operators in C++ are, to name a few:
- Arithmetic operators (+,-,*,/, %) - standard precedence and associativity rules.
- Logical and relational operators - standard precedence and associativity rules.
- Assignment operator (=) - right associative, lowest precedence.
- Increment and decrement operators (i++, ++i, i--, --i).
- Member access operator (left associative), function call, subscript (., (), []).
All these operators can be overloaded except for the last one, member access operator.
Operator overloading can be used to write the statement: a = b + c + d. However this reduces speed. The explanation is that if copy constructors any assignment operators are not used, then the operators create new methods over and over.
To circumvent the efficiency problem, one could implement block-wise algorithm which uses cache efficiently = efficient memory access pattern.
Ideas
Ideas shared in a digital bible of financial mathematics
Covering the topics of financial mathematics, almost always end up in thick text books that are a heavy burden to get through. For some people, hanging out by the computer, tablet or phone is far more interesting and in line with the evolution of today. That is why this digital bible of consumable facts come in handy.

